排序复习

快速排序

找一个哨兵，理论上是找小的放左边，找大的放右边，分成两堆，哨兵就被还原了，然后左右两边递归下去。

实际上实现的方法：

  1. 第一种最简单的方法是双指针交换法，将哨兵放到最左(右)，然后两个指针分别从开头和结尾遍历，先动尾指针，找到第一个比哨兵小的，再动头指针，找到第一个比哨兵大的，进行交换。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    void sort(vector<int>& nums,int left,int right)
    {
      if(left>=right) return ;
      int i=left,j=right,x=rand()%(right-left+1)+left;
      int t=nums[x];
      swap(nums[left],nums[x]);
      while(i<j){
        while(i<j && nums[j]>=t) j--;
        while(i<j && nums[i]<=t) i++;
        swap(nums[i],nums[j]);
      }
      swap(nums[l],nums[i]);
      sort(nums,left,i-1);
      sort(nums,i+1,right);
    }

  2. 网上叫填坑法，跟第一种类似（只不过直观程度下降了），哨兵的位置被看成是坑（缺少元素），然后每次移动这个坑。哨兵放在左边，然后先动尾指针找小于哨兵的数，填到哨兵的位置，再从左到右头指针找大于哨兵的数，填到之前的j（也就是相当于坑被移动到的上次的位置）。其实只少了swap3步操作的1步。(实际上代码没区别)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    void sort(vector<int>& nums,int left,int right)
    {
      if(left>=right) return ;
      int i=left,j=right,x=rand()%(right-left+1)+left;
      int t=nums[x];
      swap(nums[left],nums[x]);
      while(i<j){
        while(i<j && nums[j]>=t) j--;
        nums[i]=nums[j];
        while(i<j && nums[i]<=t) i++;
        nums[j]=nums[i];
      }
      nums[i]=t;;
      sort(nums,left,i-1);
      sort(nums,i+1,right);
    }

  3. 单指针直观上不太好理解，实际上也是两个指针，其中一个指针在交换时才改动，记录的是比哨兵大的位置，；首先把哨兵放到两端，左右都可以，代码中i=left-1，j=left开始，j指针往下找小于哨兵的，然后跟++i指针交换，相当于比哨兵大的数字都在i指针下面存储，然后j找到小的就跟i换。

    详情参见算法导论。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
       //哨兵没随机，取得1/2位置，以前写的代码，懒得改参数了
       void sort(int *a,int left,int right)
       {
       	if(left>=right) return ;
       	int i=left-1,j=(left+right)/2;
       	swap(a[right],a[j]);
       	int flag=a[right];
       	for(int j=left;j<right;j++)
       	{
       		if(a[j]<=flag) swap(a[++i],a[j]);
       	}
       	swap(a[++i],a[right]);
       	sort(a,left,i-1);
       	sort(a,i+1,right);
    }

理解和记忆的话，第一种最好记，但是会多一些操作，但是代码可读性高一点；第二种其次；第三种要理解指针的含义。

代码上，经过测试我倾向于在双指针移动时，将等号都写上，防止死循环，单指针应该可以不写等号。

哨兵选择建议随机。

三路快排

实际上在快排的时候，只是分成了两部分，如果遇到相等的元素，根据不同的写法会把相等的元素放到左边或者右边，这样在接下来的递归时会增加多余的操作。

三路快排的想法就是维护了三段区间，左边是<哨兵，中间是=哨兵，右边是>哨兵，那么我递归下一步，等于的区间就不动了，再递归的边界就是等于区间的左右边界。写法上，如果最左边是哨兵，用low和high指针分别维护小于区间的结尾和大于区间的开始（实际上low一直指向了哨兵）。详见算法导论。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void sort(vector<int>& nums,int l,int r){
    if(l>=r) return ;
    int i=l,j,y;
    int low=l,high=l;
    int x=rand()%(r-l+1)+l;
    int t=nums[x];
    swap(nums[l],nums[x]);
    for(j=l+1;j<=r;j++){
      if(nums[j]<t){
        //交换方式进行了改变
        y=nums[j];
        nums[j]=nums[high+1];
        nums[high+1]=nums[low];
        nums[low]=y;
        low++,high++;
      }
      else if(nums[j]==t){
        swap(nums[++high],nums[j]);
      }
    }
    sort(nums,l,low-1);
    sort(nums,high+1,r);
}

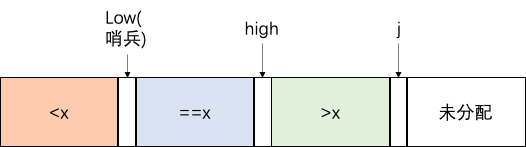
image-20210819131339162

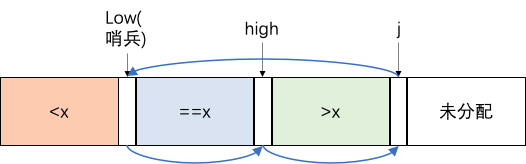
image-20210819131718039

堆

上浮，下沉这两个词确实是用的好，但是刚开始学的时候并没有接触这种说话，至今还是感觉很别扭。

插入

放到最后一个位置，然后开始上浮操作。

1
2
3
4
5
6
7
8
9
10
11
void insert(int *a,int x,int size)
{
	int tmp=size;
	a[size++]=x;
	while(tmp!=0 &&  a[tmp]<a[(tmp-1)/2])
	{
		if(tmp==0) break;
		swap(a[tmp],a[(tmp-1)/2]);
		tmp=(tmp-1)/2;
	}
}

删除

删除堆顶，把最后一个元素复制过来，下沉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int remove(int *a,int size)
{
	int top=a[0];
	a[0]=a[size-1];
	size--;
	int tmp=0;
	while(tmp<size && (a[tmp]>a[tmp*2+1] || a[tmp]>a[tmp*2+2]))
	{
		if(tmp*2+1>size || tmp*2+2>size) break;
		int tmpk=0;
		if(a[tmp*2+1]<a[tmp*2+2]) tmpk=tmp*2+1;
		else tmpk=tmp*2+2;
		if(a[tmp]>a[tmpk])
		{
			swap(a[tmp],a[tmpk]);
			tmp=tmpk;
		}
	}
	return top;
}

建堆

  1. O(n) 从所有非叶子节点的最后一个向前遍历，进行下沉。 从n/2开始向前遍历
  2. O(nlogn)从左到右不断进行上浮，相当于从0开始向堆内插入节点。

堆排序

其实就是堆顶出堆，最后一个元素放到堆顶，然后下沉。

实现方法不用额外空间的话，把最后一个元素和堆顶交换，然后下沉，沉到size-1的地方，完成一个数字的排序，依此类推。

归并排序

分成两半，每半进行排序。两半进行合并时，从两数组最小的位置开始比，每次取最小的，不断比较，最后合并完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//tmp辅助数组，[l,mid],[mid+1,r]两段合并
void merge(int l,int mid,int r)
{
	int i=l,j=mid+1,k=l;
	while(i<=mid && j<=r)
	{
		if(a[i]>a[j])
		{
			tmp[k++]=a[j++];
			coun+=mid-i+1;
		}
		else tmp[k++]=a[i++];
	}
	while(i<=mid) tmp[k++]=a[i++];
	while(j<=r) tmp[k++]=a[j++];
	for(i=l;i<=r;i++) a[i]=tmp[i];
}
void msort(int l,int r)
{
	if(l>=r) return;
	int mid=(l+r)/2;
	msort(l,mid);
	msort(mid+1,r);
	merge(l,mid,r);
}

代码实现上就是先分后排（先递归后排序）

冒泡排序

不断比相邻元素，交换。

选择排序

不断选择剩下数中最小的数字和前面交换。

插入排序

每次把一个元素插到正确的位置上。

希尔排序

每隔h取一个数，组成一个序列，获得h个序列，分别插入排序。不断减小h重复操作。